Topological Defects in Mechanical Metamaterials

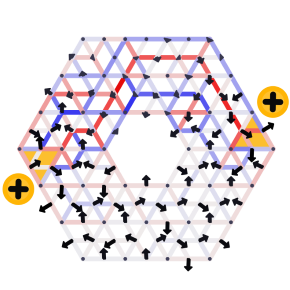topodefect[source]  Mechanical metamaterials denote an unconventional class of materials that offer an excellent platform to study various microscopic phenomena at the macroscopic level. Recently we designed and 3D-printed an anisotropic metamaterial, and by careful manipulation of only a small part of its elements, we could mimic topological defects that usually occur, e.g., in liquid crystals.

Mechanical metamaterial exhibits multiple steady states in response to periodic driving

square[source]  Pushing and pulling on a material’s surface in a steady, periodic way is a common test for characterizing that material’s mechanical properties. Simple materials typically exhibit a single steady state response to a given way of forcing. We proposed a metamaterial made of mechanically bistable elements, which responds with a wide variety of distinct steady state cycles in response to just a single, persistently applied periodic force. This metamaterial could be a step towards building materials that exhibit dynamic forms of memory in their response to periodic driving.

Each unit cell in the metamaterial spontaneously adopts one of two minimum energy deformation modes. As a result, different regions within the material settle into one or the other stable mechanical phases, analogous to competing positive and negative domains in a ferromagnet. The boundary force pattern selects the preferred mechanical phase along a given portion of the boundary.

Topology Restricts Quasidegeneracy in Sheared Square Colloidal Ice

shear_ice[source]  Physical phenomena oftentimes exhibit distinct qualitative behavior in different dimensions. So, can one make a two-dimensional system behave as in three dimensions? We introduce a simple shear transformation in a two-dimensional artificial ice, and by that we recover some of the properties of natural three-dimensional ice. Three-dimensional water ice has multiple spatial configurations of its molecules that all possess the same energy, hence the system is degenerate and it always exhibits some disorder. Its two-dimensional counterpart, the square ice, lacks such a degeneracy. By combining experiments, theory, and numerical simulations, we constructed an artificial two-dimensional ice composed of micrometer-sized colloidal particles.

Molecular Transport and Biochemical Signaling in Complex Living Tissues

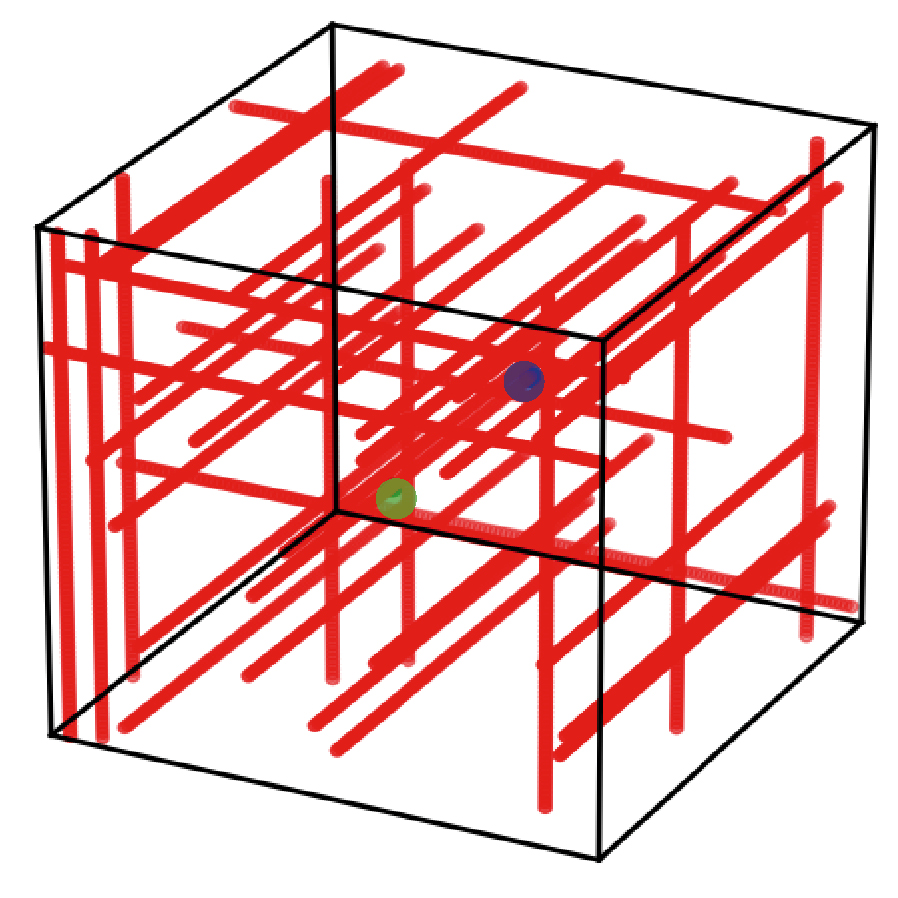fiber_lattice[source]  The extracellular matrix (ECM) is a complex and highly dynamic fibrous environment that serves as the scaffold of cells in living tissues. The ECM is an anisotropic structure that is continuously remodeled by cells, which apply mechanical forces on the fibers to generate long-range inter-cellular interactions. We propose a mechanism for biochemical-mechanical signaling feedback based on the fact that as the ECM is remodeled, molecular transport is affected.

Attraction Controls the Inversion of Order by Disorder in Buckled Colloidal Monolayers

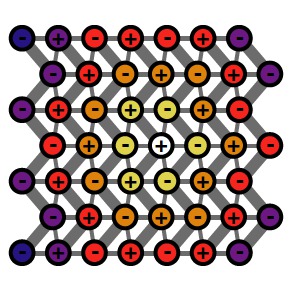bent_stripes[source] Geometrically frustrated systems cannot satisfy all local constraints, and thus, they remain disordered down to zero temperature, with a highly degenerate ground state. If entropy of fluctuations about each ground-state configuration slightly varies, then the configuration with the highest entropy will be thermodynamically selected in an order by disorder effect.

When the packing density of a buckled colloidal monolayer approaches close packing, the free-volume-dominated free energy of the system causes neighboring spheres to prefer touching opposite walls, giving rise to effective antiferromagnetic interactions.

Box Shape Determines Jamming in Confined Geometries

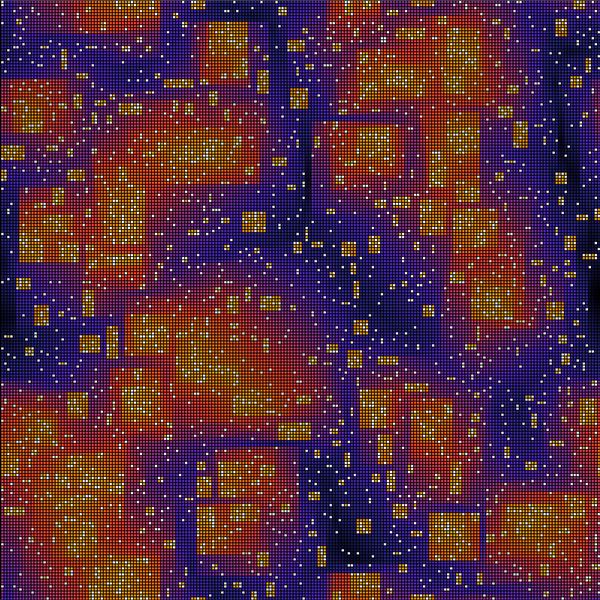frozentableAn important aspect of dense particulate matter is jamming. As the particle density increases, some particles become stuck because others block their movement. The jamming transition from a state in which almost all particles can move to a state in which almost none can move is currently attracting much interest. We theoretically investigate the effects of confinement and in particular of the system's shape on this jamming transition in granular matter and glasses, whereas previous work in the field concentrated on the behavior of particles in square or cubic systems, unconfined systems or even infinite systems.

Combinatorial Design of Textured Mechanical Metamaterials

smiley[source] We show how to assemble an astronomical number of distinct smart materials that each recognize and morph into a unique shape. To design these, we stack copies of one oriented building block, and crack the three-dimensional jigsaw puzzle that governs the placement of these blocks. We illustrate our strategy by 3D printing a metacube, which reveals a smiley pattern when compressed, and which can recognize other patterns. These novel materials bridge the gap between matter and machine, and may radically change the way in which materials can mechanically actuate and sense information, in e.g., prosthetics, wearable tech and robots.

Deformable Triangular-Lattice Antiferromagnet Models Buckled Colloidal Monolayers

frustration290x290[source] Disorder in glassy systems usually originates from geometric frustration, which arises when competing interactions may not be satisfied simultaneously. In dense arrangements of spheres, each quadruplet of particles can close-pack to form a tetrahedron. However, it is geometrically impossible to fill space with tetrahedra. For this reason particulate systems often fall into metastable disordered states (which minimize energy only locally) and fail to find the crystalline ground state (which minimizes the energy globally but not locally).

Identifying the Fingerprints of Molecular Motors in the Active Fluctuations of the Red Blood Cell Membrane

rbc290x290[source] The mechanical rigidity of cells has an important effect on their biological function, especially for red-blood cells (RBC) that have to be flexible and resilient at the same time, in order to pass unharmed through narrow capillaries in the body. The metabolic activity of the RBC controls its rigidity, and generates strong undulations of the cell membrane. The microscopic properties of the molecular motors that generate the RBC membrane activity are poorly understood.

Jamming Percolation in Three Dimensions

JP3DMany physical systems e.g. atomic or molecular systems, granular matter and colloidal suspensions, when rapidly cooled or compressed undergo a glass or jamming transition from a dynamical fluid-like state to a frozen solid-like state. Such transitions are characterized by spatial disorder accompanied by a divergent relaxation time such that structures are almost static over observation time scales. A simple way to theoretically model such non-equilibrium transitions is to use discrete lattice models with a set of kinetic rules for their dynamics. Jamming percolation models become non-ergodic even in the thermodynamic limit, contrary to other kinetically-constrained models which exhibit an apparent transition only due to finite-size effects.

Kinetically-Constrained Model Explains Dynamic Heterogeneity in Glass and Granulates

jamming290x290[source] Glass-forming liquids, granular systems, colloids, emulsions and foams exhibit a huge increase in relaxation time while their structure is hardly affected. From the analogy between the glass, or jamming, transition and other phase transitions, one would expect to find a growing correlation length governing the slow dynamics; however this length scale remains elusive. One of the leading suggestions for a relevant length scale comes from the heterogeneity of the dynamics.

Non-Equilibrium Statistical Mechanics of Dividing Cell Populations

yeast290x290[source] We suggested a model describing the dynamics of protein distributions in a proliferating cell population, motivated by chemostasis experiments on yeast in steady-state growth. Protein variation in our model is affected by a stochastic source internal to the cells and variation in division and inheritance at the population level, enabling us to assess the contribution and character of each of these components separately. We drew an analogy between the dynamics of protein distributions along cell generations and that of stress in layers of granular material.

Nonlinear Elasticity in the Interaction of Living Cells with their Mechanical Environment

traction290x290[source] The elastic cytoskeleton of biological cells contains molecular motors that produce mechanical forces by which cells attach to and pull on their surroundings. This mechanical interaction is responsible for many aspects of cellular function, from cell spreading and proliferation to stem-cell differentiation and tissue development. Both the cytoskeleton and the extracellular matrix comprise cross-linked, semi-flexible polymeric filaments, and as such they exhibit very nonlinear viscoelastic behavior that includes a power-law stiffening of the elastic moduli with increasing stress.

Relation between Structure and Dynamics in Glass-Formation

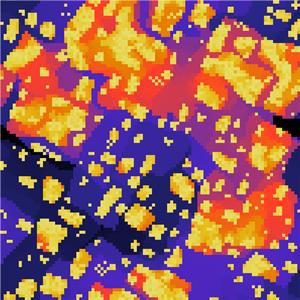PersistenceWhen cooled too rapidly, liquids fail to crystallize and fall into glassy states. Both liquids and glasses are amorphous, and structural differences between them are hard to observe. However, in a liquid the mobility of particles is dramatically larger than in the glass. Thus, although overall the structure is amorphous, in glasses there are local structures that inhibit the movement of particles inside them. One way to characterize these structures is to consider the minimum number of particles that need to move before each particle can move. In discrete kinetically-constrained models on a lattice, this structural property, the mean culling time, is easy to find by iteratively culling mobile particles from an instantaneous configuration of the system.

Shape Regulation and Elastic Interactions between Living Cells

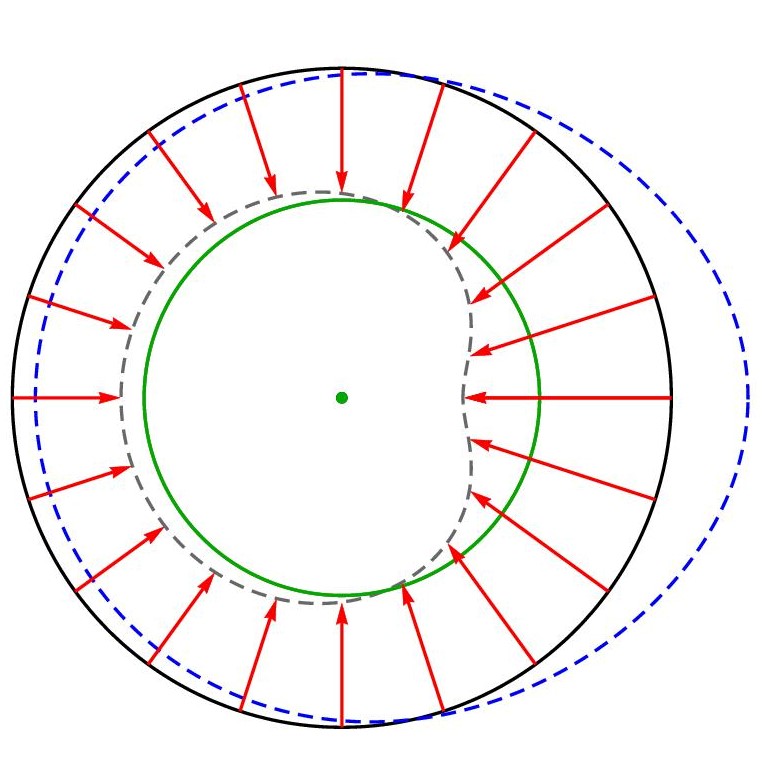fsfp_one[source] Live cells exert contractile forces, which result in elastic deformations of their environment. Cells in live tissue measure the resultant forces and displacements created on their surfaces by neighboring cells and in response correct their own forces in some preprogrammed way. To analytically calculate the interaction energy between live cells we model them as spheres surrounded by infinite material with linear elastic behavior. Each sphere in our model creates a radial deformation on its surface. If each sphere generates an isotropic displacement, the interaction energy vanishes. Thus to model real cells

Superconducting Networks

double network290x290

[source]

We calculated the magnetic-field dependence of the energy and vortex occupation for novel superconducting double network consisting of two interlaced subnetworks of small and large loops. We employ two different approaches: Mean-field analysis that minimizes the network energy assuming random-vortex configurations and numerical simulations in which energy is minimized avoiding this assumption.

Thermodynamic Analogies in Granular Materials

smallflo[source] We used molecular dynamics simulations to investigate energy distributions and spatial clustering in granular gases. Scaling arguments and mean-field calculations we performed for the granular temperature in these systems helped us gain insight on the nature of energy flow in more general driven dissipative systems. We then introduced a solvable stochastic model for dissipative interactions in generic systems, including granular materials, foams, colloidal suspensions and bacterial baths.