An important aspect of dense particulate matter is jamming. As the particle density increases, some particles become stuck because others block their movement. The jamming transition from a state in which almost all particles can move to a state in which almost none can move is currently attracting much interest. We theoretically investigate the effects of confinement and in particular of the system's shape on this jamming transition in granular matter and glasses, whereas previous work in the field concentrated on the behavior of particles in square or cubic systems, unconfined systems or even infinite systems.
We use kinetically-constrained models, which coarse-grain the system and simulate the blocking of particles by other particles. We find analytical approximations for the fraction of jammed particles for hyper-rhomboid systems in any dimension and with arbitrary lengths and particle density. In particular we find the critical density, which is the density at which for a given system size and shape the fraction of frozen particles changes from almost zero to almost unity.
We found that the corrections to the jamming critical density are not only due to the finite-size of the system, but also due to finite-density effects. This is different from many other models, and the reason is probably the infinite correlation length of the kinetically-constrained models we considered. Also, using a special property of these models, we were able to simulate systems effectively 10,000 larger than those previously simulated.
In three-dimensional systems for example, there are three main shapes: tunnels, in which one length is much longer than the other two; quasi-planes, in which one length is much shorter than the other two; and bulk, in which all three lengths are approximately the same. Because the critical density for each shape is different, changing the system's shape, without even altering its volume or the particle density, can induce jamming.
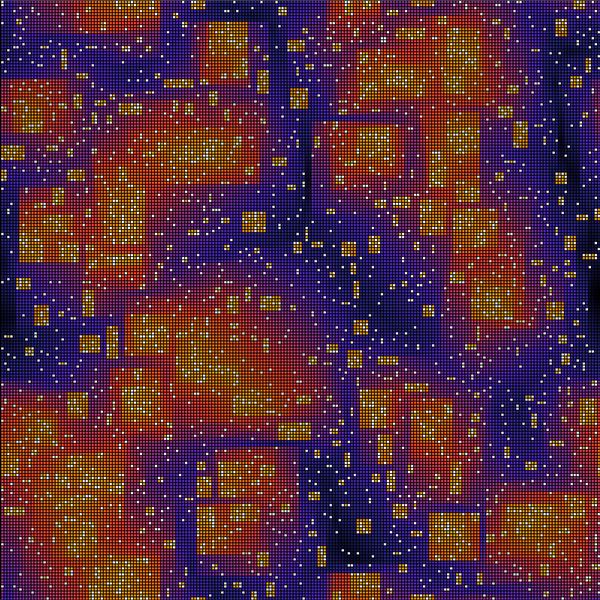
The image shows blocked particles of a kinetically-constrained model in two-dimensions: White squares are vacant. Occupied squares are colored according to the number of iterations required to remove them.
Jamming transition of kinetically-constrained models in rectangular systems
E. Teomy and Y. Shokef
Physical Review E 86, 051133 (2012)
Jamming by shape in kinetically-constrained models
E. Teomy and Y. Shokef
Physical Review E 89, 032204 (2014)
Finite-density effects in the Fredrickson-Andersen and Kob-Andersen kinetically-constrained models
E. Teomy and Y. Shokef
The Journal of Chemical Physics 141, 064110 (2014)