[source] The elastic cytoskeleton of biological cells contains molecular motors that produce mechanical forces by which cells attach to and pull on their surroundings. This mechanical interaction is responsible for many aspects of cellular function, from cell spreading and proliferation to stem-cell differentiation and tissue development. Both the cytoskeleton and the extracellular matrix comprise cross-linked, semi-flexible polymeric filaments, and as such they exhibit very nonlinear viscoelastic behavior that includes a power-law stiffening of the elastic moduli with increasing stress.
Additional nonlinearity comes from the dependence of the mechanical activity of cells on the rigidity of their environment.
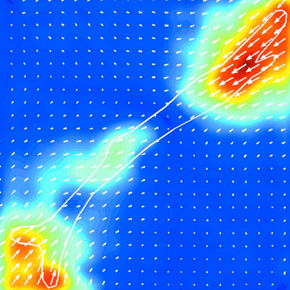
Our theoretical work is motivated by traction-force microscopy experiments of cells that adhere to soft gels, in which microbeads are used to measure the deformation field in the gel, and from which the traction forces that the cells exert are deduced. Recent experiments have shown that non-motile cells are dominated by force dipoles, comprised of equal and opposite contractile forces. However, the dependence of strain energy on the total dipole moment exhibits peculiar scaling laws which have not yet been explained.
We consider a spherical force dipole in an infinite isotropic, homogeneous, highly nonlinear elastic medium. For strong nonlinearity, the differential shear modulus diverges at a finite strain, and we may employ a small strain (but strongly nonlinear) expansion. This leads to a nonlinear differential equation for the condition of mechanical equilibrium, from which we extract scaling relations with non-trivial exponents.
Scaling laws for the response of nonlinear elastic media with implications for cell mechanics
Y. Shokef and S.A. Safran
Physical Review Letters 108, 178103 (2012)
Erratum: Scaling laws for the response of nonlinear elastic media with implications for cell mechanics
Y. Shokef and S.A. Safran
Physical Review Letters 109, 169901 (2012)